پنجشنبه, ۲۸ ارديبهشت ۱۳۹۶، ۰۶:۱۸ ب.ظ
مهدی فراهانی

پنجشنبهای به طعم ریاضی📐
"28 اردیبهشت ،
زادروز عمر خیام نیشابوری
و روز #ریاضیات خجسته باد.🌺
.
اصلا جهانی که در آن انسان باشد ولی ریاضیات نباشد قابل تصور نیست.
.
بیخود نبود که ژاکوب ژاکویی سخنی گفت:
" زندگی تنها به این درد میخورد که انسان به دو کار مشغول شود. اول #ریاضیات بخواند.
دوم ریاضیات درس بدهد."
.
🌸روز ریاضیات مبــــــــــارک🌸
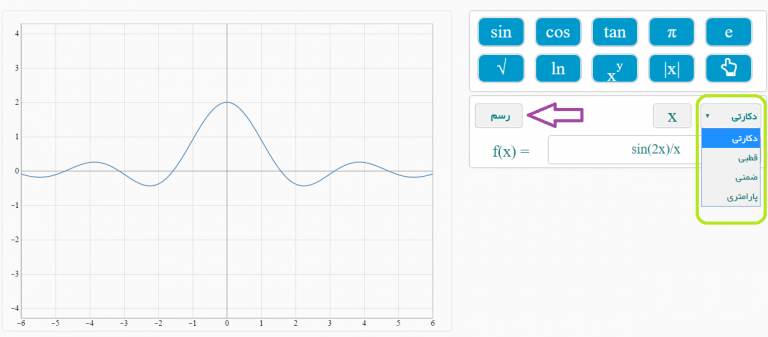
در ادامه در مورد فعالیت های خیام در زمینه ی ریاضیات را مشاهده می کنید
خیام و ریاضیات

|
|
پیش از کشف رساله خیام
در جبر، شهرت او در مشرقزمین به واسطه اصلاحات سال و
ماه ایرانی و در غرب به واسطه ترجمه رباعیاتش بوده است
و تقریباً تا حدود قرن ۱۹ میلادی از تحقیقات جبری او
اطلاعی در دست نبود. به همین دلیل کوششها و تحقیقات
خیام در علم جبر تأثیر چندانی در بسط این علم نداشته
است و در آن زمان اروپائیان در جبر به مرحلهای رسیده
بودند که آشنایی با رسالههای خیام تنها از جنبه
تاریخی برای آنها با اهمیت بوده است. قدیمیترین کتابی
که از خیام اسمی به میان آورده و نویسندهٔ آن هم عصر
خیام بوده، نظامی عروضی مؤلف «چهار مقاله» است. ولی او
خیام را در ردیف منجمین ذکر میکند و اسمی از رباعیات
او نمیآورد.
با این وجود
جورج سارتن با نام بردن از خیام
به عنوان یکی از بزرگترین ریاضیدانان قرون وسطی
چنین مینویسد:
خیام اول کسی است که به تحقیق منظم علمی در معادلات
درجات اول و دوم و سوم پرداخته، و طبقهبندی تحسینآوری
از این معادلات آورده است، و در حل تمام صور معادلات
درجه سوم منظماً تحقیق کرده، و به حل (در اغلب موارد
ناقص) هندسی آنها توفیق یافته، و رساله وی در علم جبر،
که مشتمل بر این تحقیقات است، معرف یک فکر منظم علمی
است؛ و این رساله یکی از برجستهترین آثار قرون وسطائی
و احتمالاً برجستهترین آنها در این علم است.
خیام در مقام ریاضیدان و ستارهشناس تحقیقات و
تالیفات مهمی دارد. از جمله آنها رسالة فی البراهین
علی مسائل الجبر و المقابله است که در آن از جبر
عمدتاً هندسی خود برای حل معادلات درجه سوم استفاده میکند.
او معادلات درجه دوم را از روشهای هندسی اصول اقلیدس
حل میکند و سپس نشان میدهد که معادلات درجه سوم با
قطع دادن مخروطها با هم قابل حل هستند.
برگن معتقد است که «هر کس که ترجمهٔ انگلیسی [جبر خیام]
به توسط کثیر را بخواند استدلالات خیام را بس روشن
خواهد یافت و، نیز، از نکات متعدد جالب توجهی در تاریخ
انواع مختلف معادلات مطلع خواهد شد.»
مسلم است که خیام در رسالههایش از وجود جوابهای منفی
و موهومی در معادلات آگاهی نداشته است و جواب صفر را
نیز در نظر نمیگرفته است.
یکی دیگر از آثار ریاضی خیام رسالة فی شرح ما اشکل من
مصادرات اقلیدس است. او در این کتاب اصل موضوعهٔ پنجم
اقلیدس را دربارهٔ قضیهٔ خطوط متوازی که شالودهٔ هندسهٔ
اقلیدسی است، مورد مطالعه قرار داد و اصل پنجم را
اثبات کرد.به نظر میرسد که تنها نسخه کامل باقیمانده
از این کتاب در کتابخانه لیدن در هلند قرار دارد.
درکتاب دیگری از خیام که اهمیت ویژهای در تاریخ
ریاضیات دارد رسالهٔ مشکلات الحساب (مسائلی در حساب)
هرچند این رساله هرگز پیدا نشد اما خیام خود به این
کتاب اشاره کرده است و ادعا میکند قواعدی برای بسط
دوجملهای (a + b)n کشف کرده و اثبات ادعایش به روش
جبری در این کتاب است.
به هر حال قواعد این بسط تا n = 12 توسط طوسی (که
بیشترین تاثیر را از خیام گرفته) در کتاب «جوامع
الحساب» آورده شده است.[
روش خیام در به دست آوردن ضرایب منجر به نام گذاری
مثلث حسابی این ضرایب به نام مثلث خیام شد، انگلیسی
زبانها آن را به نام مثلث پاسکال میشناسند که البته
خدشهای بر پیشگامی خیام در کشف روشی جبری برای این
ضرایب نیست.
خیام به تحلیل ریاضی موسیقی نیز پرداخته است و در
القول علی اجناس التی بالاربعاء مسالهٔ تقسیم یک چهارم
را به سه فاصله مربوط به مایههای بینیمپرده، با نیمپردهٔ
بالارونده، و یک چهارم پرده را شرح میدهد.
مهمترین دستآوردها:
ابداع نظریهای دربارهٔ نسبتها همارز با نظریهٔ
اقلیدس.
«در مورد جبر، کار خیام در ابداع نظریهٔ هندسی معادلات
درجهٔ سوم موفقترین کاری است که دانشمندی مسلمان انجام
داده است.»
او نخستین کسی بود که نشان داد معادلهٔ درجهٔ سوم ممکن
است دارای بیش از یک جواب باشد و یا این که اصلا جوابی
نداشته باشند.«آنچه که در هر حالت مفروض اتفاق میافتد
بستگی به این دارد که مقاطع مخروطیای که وی از آنها
استفاده میکند در هیچ نقطه یکدیگر را قطع نکنند، یا
در یک یا دو نقطه یکدیگر را قطع کنند.»
«نخستین کسی بود که گفت معادلهٔ درجهٔ سوم را نمیتوان
عموما با تبدیل به معادلههای درجهٔ دوم حل کرد، اما
میتوان با بکار بردن مقاطع مخروطی به حل آن دست یافت.»
«در نیمهٔ اول سدهٔ هیجدهم، ساکری اساس نظریهٔ خود را
دربارهٔ خطوط موازی بر مطالعهٔ همان چهارضلعی دوقائمهٔ
متساویالساقین که خیام فرض کرده بود قرار میدهد و
کوشش میکند که فرضهای حاده و منفرجهبودن دو زاویهٔ
دیگر را رد کند.»
|
|
**
|
|
مثلث
خیام ـ پاسکال
یکی از زیباترین نگارههای عددی است که در تاریخ
ریاضیات مورد توجه ریاضیدانان قرار گرفته است.
1
1 1
۱ ۲ ۱
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
و........
به سهولت مشخص میشود که هر سطر با سطر بالاتر از خود
چه رابطهای دارد.
یکی از خواص این مثلث آن است که مجموع اعداد هر سطر
برابر است با توانهای از صفر تا nعدد 2
حال به بسط دوجملهای خیام ـ نیوتن توجه کنیم:
(a+b)0= 1
(a+b)1= a+b
(a+b)2= a2+2ab +b2
(a+b)3= a3+3a2b + 3ab2+ b3
(a+b)4= a4+4a3b +6a2b2 +4ab3 + b4
(a+b)5= a5+5a4b + 10a3b2+ 10a2b3+ 5ab4+ b5
(a+b)6= a6+ 6a5b+ 15a4b2+ 20a3b3 + 15a2b4+ 6ab5+ b6
و ...
اگر به ضرایب بسط دو جملهای توجه شود، همان اعداد
مثلث فوقالذکر هستند. یا به عبارتی اگر به جای a و
b عدد 1 گذاشته شود، این بسط، همان مثلث فوق را تشکیل
میدهد.
خیام برای حل معادلات درجۀ اول و دوم و سوم آنان را به
ترتیب زیر طبقهبندی کرد.
(معادلاتی که با علامت * مشخص شدهاند، قبل از خیام حل
شده بودند.)
1- معادلات دوجملهای
* a= x
* a= x2
a= x3
* ax= x
ax2= x3
ax= x3
2- معادلات سه جملهای
* x2+ax= b
* x2+b= ax
* x2= ax+b
* x3+ax2= bx
* x3+bx= ax2
* x3= ax2+bx
1- x3+bx= c
2- x3+c= bx
3- x3= bx+c
4- x3+ax2= c
5- * x3+c= ax2
6- x3= ax2+c
3- معادلات چهار جملهای
7- x3+ax2+bx= c
8- * x3+ax2+c= bx
9- x3+bx+c= ax2
10- x3= ax2+bx+c
11- x3+ax2= bx+c
12- x3+bx= ax2+c
13- x3+c= ax2+bx
از این 25 نوع معادله، راهحل 11 نوع آن، قبل از خیام
پیدا شده بود. خیام درستی معادلات حل شده را آزمود و
برای بقیۀ معادلهها یا راهحل جبری و هندسی و یا تنها
راه حل هندسی یافت. از آن میان 13 نوع آخر (معادلات
درجۀ سوم) را با استفاده از مقاطع مخروطی حل کرد.
راهحلِ جبری معادلات درجۀ سوم و چهارم آن طور که
محققین تاریخ علم ریاضی معتقدند، همان راه حل هندسی
خیام برای معادلات درجۀ سوم، با استفاده از مقاطع
مخروطی است.
استاد دکتر محسن هشترودی چگونگی استفادۀ اروپائیان را
از روش خیام در اختیار ما گذاشته است:
معادلۀ درجۀ سوم را با ضرب کردن در x به معادلۀ درجۀ
چهارم تبدیل میکنیم. (پس از خاتمۀ کار ریشۀ x= 0 را
کنار میگذاریم.)
معادلۀ درجۀ چهارم:
x4+ax3+bx2+cx=0
را با تبدیل
x y-a/4 =
میتوان به معادلۀ
y4+Ay2+By+C=0
تبدیل کرد. روشن است که تبدیل بالا جهت حذف توان سوم
مجهول در معادله بوده است. حال چون برای سهولت y را
به x نشان دهیم، معادله به صورت زیر نوشته میشود.
(ß)
x4+Ax2+Bx+C=0
در این معادله x2= y را جانشین میکنیم. حل معادله
(ß) به حل دستگاه دو معادلۀ دو مجهولی زیر (دستگاه
شمارۀ 1) منجر میشود:
x2=y
y2+Ay+Bx+C=0
از نظر هندسی مسئله به تقاطع دو سهمی بدل میشود که
محورهای آنها بر هم عمودند؛ زیرا محور سهمی اول یعنی
x2=y محور oy میباشد و محور سهمی دوم یعنی
Y2+Ay+Bx+C=0
موازی با ox است.
این دو سهمی دارای چهار نقطۀ تقاطع (حقیقی یا موهومی)
می باشند که بر یک دایره واقعند. (این را هم خود خیام
ثابت کرده است که نقاط تقاطع دو سهمی روی یک دایره
واقع می شوند.) و میتوان به سهولت با افزودن دو
معادلۀ دستگاه شمارۀ 1 ، معادلۀ دایره را تعیین کرد.
یعنی دستگاه شمارۀ 1 و دستگاه شماره 2 (دستگاه زیر)
دارای جوابهای یکسان هستند.
x2= y
(A-1)y+Bx+c=0 x2+y2 +
که معادلۀ دوم دستگاه شمارۀ 2 مجموع دو معادلۀ دستگاه
شمارۀ 1 میباشد. و مشاهده میشود که تعیین ریشههای
معادلۀ درجۀ چهارم (ß) به تعیین نقاط تقاطع دایرۀ :
(A-1)y+Bx+c=0 x2+y2 +
با سهمی x2= yمنجر میشود که طول نقاط تقاطع، چهار
ریشۀ معادلۀ (ß) میباشند. به طریق هندسی حل دستگاه
شمارۀ 1 یعنی تقاطع دو سهمی که محورهای آنها بر هم
عمودند، به تقاطع یکی از این سهمیها با دایرۀ مذکور
بدل میشود و این مطلب از استنباطهای خیام در حل
معادلات درجۀ سوم نتیجه شده است.
|
|
**
بخشی از
مقاله خانم فرزانه آقائی پور
|
۹۶/۰۲/۲۸
 ۱
۱
 ۰
۰
مهدی فراهانی










![29 خرداد سالروز درگذشت[شهادت] دکتر علی شریعتی](http://bayanbox.ir/view/8796745227418745234/Shariati.jpg)